Μαθαίνω την προπαίδεια

Α΄ περίοδος

**τεθλασμένη (ορισμός)

**περίμετρος (έννοια)

**ΑΝΑΠΤΥΓΜΑ ΚΥΒΟΥ

**ravdogramma ΓΙΑ ΤΟ ΚΕΦ. 6

*Κεφ. 10 άσκ 2 σελίδα 29 (Συμπληρώνω το πρόβλημα *κάθε λεωφορείο μπορεί να μεταφέρει 35 καθιστούς και 48 όρθιους επιβάτες)

**Λύνω με δύο τρόπους τα παρακάτω προβλήματα  προβλήματα  για το κεφάλαιο 10

Κεφάλαιο 11

**οδηγίες κάθετης διαίρεσης, διάκριση διαίρεσης μέτρησης – μερισμού

**πότε κάνω διαίρεση

Κεφάλαιο 12

Μαθαίνω την (ευκλείδεια) διαίρεση !

θεωρία για την Ευκλείδεια διαίρεση

2η επανάληψη

ΚΡΙΤΗΡΙΑ ΔΙΑΙΡΕΤΟΤΗΤΑΣ

Κεφάλαιο 15.

Θυμάμαι τους δεκαδικούς αριθμούς

Κανόνας:

Για να μετατρέψουμε ένα δεκαδικό κλάσμα σε δεκαδικό αριθμό, γράφουμε τον αριθμητή όπως είναι και μετράμε τα μηδενικά του παρονομαστή. Μετά μετράμε ίδιο αριθμό ψηφίων στον αριθμητή αρχίζοντας από δεξιά προς τα αριστερά, για να βάλουμε την υποδιαστολή. Π.χ.:

Πηγή: http://users.sch.gr/parantoniou/site/matimatika/maths_kef35.html

κεφάλαιο 17

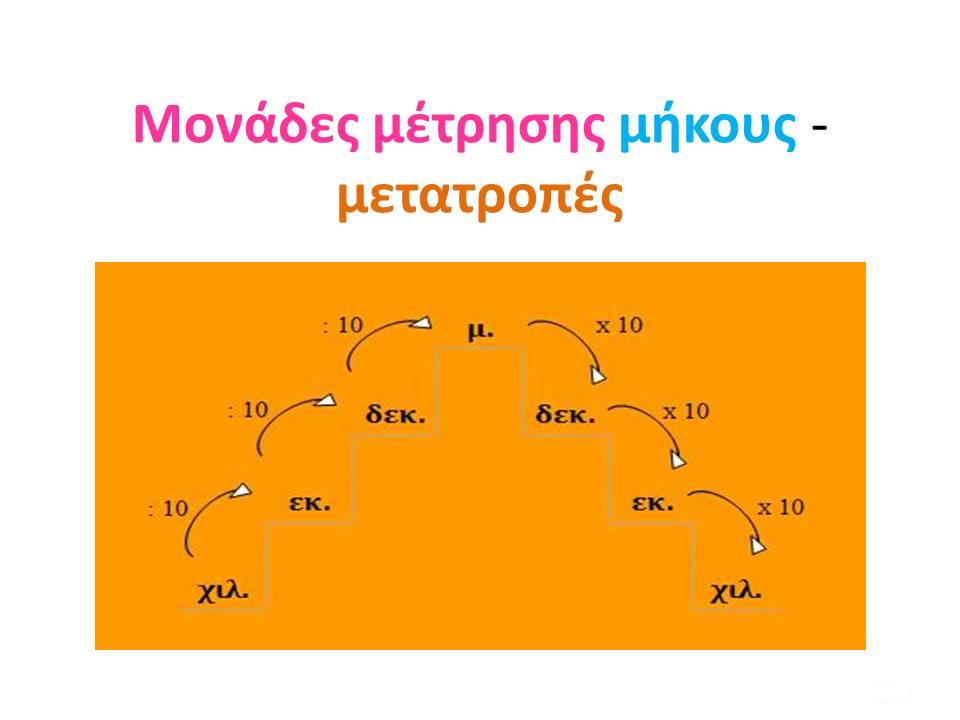
μονάδες μέτρησης μήκους – μετατροπές

ΠΡΟΕΤΟΙΜΑΣΙΑ ΓΙΑ ΤΟ ΕΠΑΝΑΛΗΠΤΙΚΟ ΤΗΣ 3ης ΕΝΟΤΗΤΑΣ   (ΒτΜ σελ. 52. ΤΕ σελ.18)

κεφάλαια 21-26

Προβλήματα με σχεδιαγράμματα

27. κάθετες, παράλληλες ευθείες, περίμετρος, εμβαδόν

Μαθαίνω πώς να σχεδιάζω μια κάθετη ευθεία (πατάω στον πίνακα συνέχεια “σχεδίασε” για να μάθω βήμα βήμα πώς να σεδιάσω)

Κάθετες ευθείες, παράλληλες ευθείες, ορθές γωνίες

32. ΜΑΘΑΙΝΩ ΓΙΑ ΤΑ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΑ

ΘΕΩΡΊΑ

τετράγωνο – ρόμβος (διαφορές ομοιότητες)

παραλληλόγραμμα – εφαρμογή

5η επανάληψη

ΟΜΟΙΟΤΗΤΕΣ ΚΑΙ ΔΙΑΦΟΡΕΣ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ

Κοίταξε καλά τα τετράπλευρα και διαβάστε  τις ομοιότητες και τις διαφορές τους:

Α)

ΤΕΤΡΑΓΩΝΟ                                                               ΟΡΘΟΓΩΝΙΟ

    Ομοιότητες: .Έχουν τις πλευρές τους ανά δυο παράλληλες. Έχουν τέσσερις ορθές γωνίες.

Διαφορές: Το τετράγωνο έχει τέσσερις πλευρές ίσες ενώ το ορθογώνιο έχει τις πλευρές του ανά δυο ίσες.

 Β)

 ΤΕΤΡΑΓΩΝΟ                                   ΡΟΜΒΟΣ

Ομοιότητες: Έχουν τις πλευρές τους ανά δυο παράλληλες. Έχουν και τις τέσσερις πλευρές τους ίσες.

Διαφορές: Το τετράγωνο έχει τέσσερις γωνίες ίσες (ορθές) ενώ ο ρόμβος  έχει τις γωνίες του ανά δυο ίσες

Γ)

ΟΡΘΟΓΩΝΙΟ                                         ΠΛΑΓΙΟ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΟ

Ομοιότητες: Έχουν τις πλευρές τους ανά δυο παράλληλες και ίσες.

Διαφορές: Το ορθογώνιο  έχει τέσσερις γωνίες ίσες (ορθές) ενώ το πλάγιο παραλληλόγραμμο   έχει τις γωνίες του ανά δυο ίσες

Δ)                          

        ΡΟΜΒΟΣ                  ΠΛΑΓΙΟ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΟ

Ομοιότητες: Έχουν τις πλευρές τους ανά δυο παράλληλες . Οι γωνίες τους είναι ανά δυο ίσες.

Διαφορές:  Ο ρόμβος  έχει τέσσερις πλευρές ίσες ενώ το πλάγιο παραλληλόγραμμο  έχει τις πλευρές του ανά δυο ίσες.

κεφ. 33 υπολογίζω περιμέτρους καεμβαδά

υπολογισμοί online

5 κριτήριο

προετοιμασία για το επαναληπτικό που θα γράψουμε αύριο. (5o_kritirio)

http://3dim-megar.att.sch.gr/index.php/home

42. Διαιρώ με διψήφιο διαιρέτη

Η παρακάτω παρουσίαση δείχνει αναλυτικά τα βήματα εκτέλεσης μιας διαίρεσης .Κάνε κλικ εδώ και δείτε την!

επαναληπτικές ασκήσεις για τα κεφάλαια 41-45 στα μαθηματικά

κεφ.52 Μαθαίνω για τα στερεά

κεφ. 53

ευθείες, παράλληλες ευθείες, ορθές γωνίες

Κάθετες ευθείες

Με το γνώμονα (το τριγωνάκι μας) ελέγχουμε αν δύο ευθείες είναι κάθετες μεταξύ τους.

Τοποθετούμε το γνώμονα -με τις κάθετες πλευρές του- ανάμεσα στις δύο ευθείες. Αν οι πλευρές του γνώμονα ακουμπάνε πάνω στις ευθείες, τότε είναι κάθετες (σχήμα α). Αν δεν ακουμπάνε πάνω στις ευθείες, δεν είναι κάθετες (σχήματα β, γ, δ).

Ορθές γωνίες

Όταν δύο ευθείες είναι κάθετες μεταξύ τους, η γωνία ή οι γωνίες που σχηματίζονται λέγονται ορθές. Και συμβολίζονται όπως βλέπεις στο σχήμα.

Παράλληλες ευθείες

Δύο ευθείες είναι παράλληλες όταν, όσο κι αν τις προεκτείνουμε (μεγαλώσουμε), δεν πρόκειται να συναντηθούν ποτέ.